
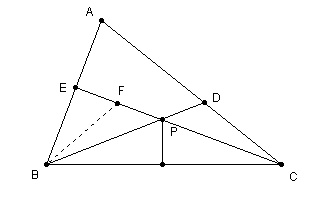
因为 P为△ABC的BC边垂直平分线上的一点, 所以 ∠PBC=∠PCB
∠BPE = ∠PBC+∠PCB = 2∠PBC = ∠A
∠EPD 与 ∠A 互补
∠AEP 与 ∠ADP 互补
∠BEC 与 ∠BDC 互补
在PE上取一点F, 令PF = PD, 连接BF
因为∠BPF = ∠CPD, BP=CP, PD=PF
所以 BF=CD, 并且∠BFP = ∠CDP;
因为∠BEC 与 ∠BDC(∠CDP) 互补
所以∠BEC 与 ∠BFP 互补
∠BEC= ∠BFE
BE=BF
所以BE=BF=CD
[
本帖最后由 一叶轻舟 于 2008-4-5 10:13 编辑 ].