13楼一叶轻舟
(点击左侧我的网站,光临我的博客......)
发表于 2008-7-11 08:13
只看此人
证法三 (利用勾股定理)
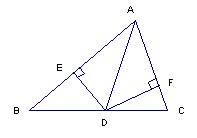
过D作AB, AC的高, 垂足为E, F
显然 △AED全等于△AFD ==> AE = AF, ED = FD
又根据勾股定理可得:
AD^2 = AE^2 + ED^2 ------ (1)
BD^2 = BE^2 + ED^2 = (AB - AE)^2 + ED^2 = AB^2 + AE^2 - 2AB*AE + ED^2 ------ (2)
CD^2 = CF^2 +DF^2 = (AC - AE)^2 + ED^2 = AC^2 + AE^2 - 2AC*AE + ED^2 ------ (3)
由(2),(3)整理得: (AB^2 + AE^2 + ED^2 - BD^2) / AB = (AC^2 + AE^2 + ED^2 - CD^2) / AC ------ (4)
将(1)代入(4)得: (AB^2 + AD^2 - BD^2) * AC = (AC^2 + AD^2 - CD^2) * AB
进一步整理后得: AB* AC * (AB - AC) - AD^2 * (AB - AC) - BD^2 * AC + CD^2 * AB ------ (6)
再根据角平分线及正弦定理可知: AB / AC = BD / CD 即AB * CD = AC *BD ------ (5)
将(5)代入(6)得: AB* AC * (AB - AC) - AD^2 * (AB - AC) - BD * CD * (AB - AC) =0
即 AB* AC - BD * CD = AD^2
[ 本帖最后由 一叶轻舟 于 2008-7-11 08:18 编辑 ].
附件
-
 a.jpg
(4.84 KB)
a.jpg
(4.84 KB)
-
2008-7-11 08:18