ABCD为平行四边形，圆O过A点且与AB，AC及AD的延长先交于P，Q，R，求证：AP×AB+AR×AD=AQ×AC
。.

您这些天出的题貌似难了点, 俺的水平仅停留在捣鼓三角形内外心的水平上,圆也没接触到呢, 能否出些有关三角形五心的题目练练呀?

折腾老半天, 还查了下有关圆的性质定理, 终于有了眉目
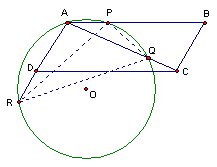
首先根据一个叫"托勒密"的定理, 圆内接四边形(APQR)对边乘积的和= 对角线的乘积
即:AP * RQ + AR * PQ = AQ * PR ------ (1)
再由 ∠BAC = ∠PRQ, ∠ACB = ∠CAR = RPC ====> △ABC 相似于 △RQP ====> PQ/BC = RQ/AB = RP/AC = k
于是, PQ = BC * k, RQ = AB * k, RP = AC * k ------ (2)
将(2)代入(1)得
AP * AB * k + AR * BC * k = AQ * AC * k
而 BC = AD
∴ AP * AB + AR * AD = AQ * AC.

老猫出好题，轻舟露身手。我来用劲鼓掌！ .