2楼一叶轻舟
(点击左侧我的网站,光临我的博客......)
发表于 2008-8-21 09:35
只看此人
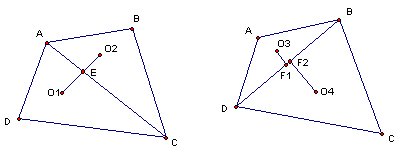
设△ADC的内心为O1, △ABC的内心为O2, O1在AC边上的射影为E
∵△ADC与△ABC的内切圆外切
∴E也为O2在AC边上的射影
∴AE 既 = (AC+AB-BC)/2, 又 = (AC+AD-DC)/2
∴ AB-BC = AD-DC ---- (1)
同样设△ABD的内心为O3, △BCD的内心为O4, O3在BD边上的射影为F1, O4在BD边上的射影为F2
那么BF1 = (BD+AB-AD)/2, BF2 = (BD+BC-DC)/2
由(1)式可知: AB-AD=BC-DC
∴BF1=BF2
即F1与F2重合
则△ABD与△BCD的内切圆也外切
-----------------------------------------------------------------------------------
申明: 本题借助了8/15 (ITmeansit) 的思路,是站在了巨人的肩膀上
[ 本帖最后由 一叶轻舟 于 2008-8-21 09:51 编辑 ].
附件
-
a.jpg
(11.38 KB)
-
2008-8-21 09:51
