几道抽屉原理的数学题，请各位高手不吝赐教：
1）对于任意的正整数n，证明必存在一个完全由0或5组成的整数，它是n的倍数。

2）已知平面上有31个点，其中任何三点中总有两个点的距离小于1，求证：可用一个半径为1的圆盖住其中的16个点。

3）求证：任意给定6个正整数，用适当的运算符号联结起来后，必可使其运算的结果是30 的倍数。

4）已知9条直线中的每一条均把同一个正方形分成面积之比为2：3的两个四边形，证明：这9条直线中至少有3条过同一个点。.

1、在n+1个正整数：5、55、555、...、55...55中，其中一定有两个数除以n的余数相同，相减即可。

2、取最远的两点。若其距离小于1，搞定。若其距离大于1，则这两点只作为圆心，画两个半径为1的圆，也搞定。

3、六个数中有两个数除以5的余数相同，相减。剩下四个数中有两个数除以3的余数相同，相减。剩下两个数，若有一个是偶数，将前面两个差和剩下两个数相乘即可；若都是奇数，相减，然后和前面的两个差相乘即可。

4、满足要求的直线一定经过正方形中的四个点之一，所以搞定。这四个点是对称的，但是说起来比较麻烦。偷懒了。.

引用:

原帖由 老猫 于 2008-8-25 22:06 发表
1、在n+1个正整数：5、55、555、...、55...55中，其中一定有两个数除以n的余数相同，相减即可。

2、取最远的两点。若其距离小于1，搞定。若其距离大于1，则这两点只作为圆心，画两个半径为1的圆，也搞定。

3、 ...

还是老猫的速度快，我才看到。.

谢谢猫老师指点迷津。最后一题我还要再深刻领悟一下。.

第4题给你一个详细版的，希望对你有用：
证明：设正方形为ABCD，E、F分别是AB，CD的中点。 设直线L把正方形ABCD分成两个梯形ABGH和CDHG，并且与EF相交于 P.梯形ABGH的面积：梯形CDHG的面积=2∶3,EP是梯形ABGH的中位线，PF是梯形CDHG的中位线，由于梯形的面积=中位线×梯形的高， 并且两个梯形的高相等（AB=CD），所以梯形ABGH的面积∶梯形CDHG的面积=EP∶PF，也就是EP∶PF=2∶3 .这说明，直线L通过EF上一个固定的点P，这个点把EF分成长度为2∶3的两部分。这样的点在EF上还有一个，如图上的Q点（FQ∶QE=2∶3）。同样地，如果直线L与AB、CD相交，并且把正方形分成两个梯形面积之比是2∶3，那么这条直线必定通过AD、BC中点连线上的两个类似的点（三等分点）。这样，在正方形内就有4个固定的点，凡是把正方形面积分成两个面积为2∶3的梯形的直线，一定通过这4点中的某一个。我们把这4个点看作4个抽屉，9条直线看作9个苹果，由定理2可知，9=4×2+1，所以，必有一个抽屉内至少放有3个苹果，也就是，必有三条直线要通过一个点。

222.JPG (5.94 KB)

2008-8-25 23:11

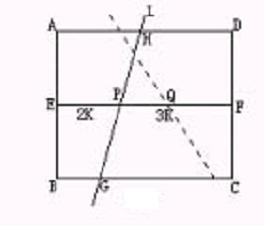
说明：本题中的抽屉比较隐蔽，正方形两双对边中点连线上的4个三等分点的发现是关键，而它的发现源于对梯形面积公式S梯形=中位线×梯形的高的充分感悟。.

谢谢，很详细，很清楚。.

引用:

原帖由 罗小星 于 2008-8-25 22:22 发表


还是老猫的速度快，我才看到。

不是我速度快，是发帖的时间准。
我睡觉前看一下而已。
：）
写完就睡觉去了。.