引用:
原帖由 Jupiter 于 2009-1-7 23:23 发表 
刚才给儿子检查最后一张练习卷,有这样一道填空题:一个直角三角形,三条边分别是7厘米,10厘米,6厘米,它的面积是多少。。。21平方厘米。
这没有啥稀奇的,但是我这个多事的老娘又想加菜,炫耀自己本领,告诉儿子 ...
哈哈哈哈,BS这个老师。如果能跟儿子一起证明这道题是错误的,那对孩子来说实在是妙不可言。
前面我跟儿子证明了老师出的幻方错误了,儿子非常得意:同学们都发现了这个错误,而只有他一人证明了错误。
可以从下面几个方面考虑:
1、直角三角形的面积是长方形的一半。
2、这个长方形如果保持低边和高的长度不变,拉伸以后的平行四边形面积也不变。
3、与正确的勾三股四弦五进行比较,也许能证明这道题是错误的。(貌似是几何意义上的,不能确定)
建议找高手出马,先设计好。着魔了,搞到半夜1点,躺床上翻来覆去想,总也不能绕过勾股定理。后来也想通了,何必这么累,绕不过,就证明呗。
我们都学过勾股定理,还真没证明过。中学学的时候,老师可能觉得同学们理解不了,没教。到了大学,老师是正经八百的孔子门徒,“不叩不响”。
喜欢婆什迦罗的证明。
==================
【转贴】勾股定理的证明
勾股定理是数学中最重要的定理之一。也许在数学中还找不到这样一个定理,其证明方法之多能够超过勾股定理。它有四百多种证明!卢米斯(Loomis)在他的《毕达哥拉斯定理》一书的第二版中,收集了这个定理的37O种证明并对它们进行了分类。
勾股的发现
关于这个定理,虽然号称毕达哥拉斯定理,但人们在遗留下来的古希腊手稿或译文中并没有找到毕达哥拉斯本人及其学派的有关证明,所以人们只能对他可能用的方法进行一些揣测。有据可查的最早证明见于欧几里得的《几何原本》(公元前3世纪)之中。欧几里得用几何的方法,作出了一个巧妙的证明,有兴趣的读者不妨查阅一下。
中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。赵爽创制了一幅“勾股圆方图”,用形数结合的方法,给出了勾股定理的详细证明。在这幅“勾股圆方图”中,以弦为边长得到正方形ABDE是由4个全等的直角三角形再加上中间的那个小正方形组成的。每个直角三角形的面积为ab/2;中间的小正方形边长为b-a,则面积为(b-a)2。

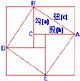
于是便可得如下的式子:
4×(ab/2)+(b-a)2=c2
化简后便可得:
a2+b2=c2
亦即:
c=(a2+b2)(1/2)
赵爽的这个证明可谓别具匠心,极富创新意识。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范。以后的数学家大多继承了这一风格并且有所发展。
印度的数学家兼天文学家婆什迦罗,也给出了与赵爽相同的几何图形。但是婆什迦罗在画出这个图形之后,并没有进一步解释和证明,只是说:“正好!”婆什迦罗还给出了这个定理的另外一个证明,即画出斜边上的高,由图中给出的两个相似三角形,我们有

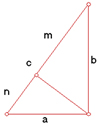
c/b=b/m和c/a=a/n
即
cm=b2和cn=a2
相加便得:
a 2 +b2=c(m+n)=c2
勾股的证明
中国的数学家刘徽在证明勾股定理时也是用的以形证数的方法,只是具体图形的分合移补略有不同而已。刘徽对这组公式进行了严格的论证。这是迄今为止用于勾股数的最完美的表达形式之一。
勾股趣事
汉朝的数学家赵君卿,在注释《周髀算经》时,附了一个图来证明勾股定理。这个证明是四百多种勾股定理的说明中最简单和最巧妙的。您能想出赵老先生是怎样证明这个定理的吗?
中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位。尤其是其中体现出来的“形数统一”的思想方法,更具有科学创新的重大意义。事实上,“形数统一”的思想方法正是数学发展的一个极其重要的条件。正如当代中国数学家吴文俊所说:“在中国的传统数学中,数量关系与空间形式往往是形影不离地并肩发展着的......十七世纪笛卡儿解析几何的发明,正是中国这种传统思想与方法在几百年停顿后的重现与继续。”
附件为勾股定理的16种证明方法
[
本帖最后由 ccpaging 于 2009-2-26 12:38 编辑 ].